Homeworks to do

1.3 – Constructing of Ellipse 

1.3.1 – Ellipses/Ovals

An ellipse (Greek “elleipsis” - a "falling short") is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve, (See Fig.27).

                                                                    

                                       Fig.27 – An ellipse obtained as the intersection of a cone with a plane

There are several methods whereby an ellipse can be drawn, by given the length of its major and minor axes:

a) The Auxiliary Circle Method

·         Steps 1 – Draw the major axis AB. Draw a circle by taking radius of OA from centre O.

·         Steps 2 – Draw another circle whose diameters are the minor axis. Point CD is form by erect a perpendicular line from O. Now A, B, C and D are points on the ellipse. The next task is to find the position of the other points on the ellipse and then to join them together.

·         Steps 3 – Divided those circle into a convenient number of parts (preferably 12 parts). This can be easily done using the 30°/60° set square.

·         Steps 4 – Draw horizontal and vertical lines at where the big circle and small circle met with the 12 parts line. The intersection of the horizontal and vertical line becomes a point on the ellipse.

·         Steps 5 – Plot all those point together to draw the ellipse. This can be done with “French curve” or “Flexible curve” or “Freehand” method.

b) The Rectangle Method/Radial Line Method

·         Steps 1 – Draw the major axes AB and minor axes CD respectively, intersecting at O.

·         Steps 2 – Produce a rectangle by drawing EF and GH both parallel to AB, and EG and FH parallel to CD respectively.

·         Steps 3 – Divided OA and OB into the same number of equal parts (preferably 4 parts) and numbering the points 1,2,3 and 4 as shown. This can be done by using “division of line method”.

·         Steps 4 – Draw radial line from D and C through point 1, 2, 3 and 4 on line OA and OB.

·         Steps 5 – Divided AE, AG, BF and BH into the same number of equal parts (preferably 4 parts) and numbering the points 1,2,3 and 4 as shown. This can be done by using “division of line method”.

·         Steps 6 – Draw radial line from D and C through point 1, 2, 3 and 4 on line AE, AG, BF and BH. The intersection of the above line becomes a point on the ellipse.

·         Steps 7 – Plot all those points together to draw the ellipse. This can be done with “French curve” or “Flexible curve” or “Freehand” method.

                                      

                              

c) The Four Arc Method

There are occasions when it is not essential that an ellipse on a drawing can be shown with a great accuracy. Although this is only approximate but it is permissible to use this method since it can be drawn using straight edge and compasses only.

·         Steps 1 – Draw the major axes AB and minor axes CD respectively, intersecting at O.

·         Steps 2 – Produce a rectangle by drawing EF and GH both parallel to AB, and EG and FH parallel to CD respectively.

·         Steps 3 – Join ED

·         Steps 4 – Bisect AE to find point J and join JC. Point K is result from he intersecting of line JC and ED.

·         Steps 5 – Join AK and bisect it at right angles. The bisecting line LM cuts on line AB producing point N.

·         Steps 6 – Bisect line KC at right angles. The bisecting line PQ cuts on line CD producing point R.

·         Steps 7 – With centre R and radius from RC, draw an arc from point C to point K.

·         Steps 8 – With centre N and radius from NA, draw an arc from point A to point K.

·         Steps 9 – By stepping off CS equal to DR, and BT equal to AN, we then have the four centres N, R, S and T from which we can drawn four arcs to produce a good approximation of the ellipse.

(Note: Only a good compass can produce a very accurate approximation of this method.)

                                      

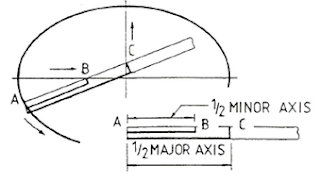
d) The Trammel Method

·         For this method, you must have “a thick paper and a scissor”.

·         The measurements of the major and minor axis are provided.

·         The formula for this method are; Point AC = ½ of the Major Axis, and Point AB = Minor Axis.

·         Draw a trammel on a thick paper by applying the above formula. Once done, and then cut the trammel.

·         Trace/point out the path of the ellipse using the end of point A as a guide. During this process, make sure that the points B and C on the trammel must always touch the major and minor axes.